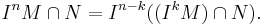Artin–Rees lemma
In mathematics, the Artin–Rees lemma (also known as the Artin–Rees theorem) is a result in the theory of rings and modules. It was proved in the 1950s in independent works by the mathematicians Emil Artin and David Rees; a special case was known to Oscar Zariski prior to their work. The result is used to prove the exactness property of completion(Atiyah & MacDonald 1969, pp. 107–109).
Statement of the result
Let I be an ideal in a Noetherian ring R; let M be a finitely generated R-module and let N a submodule of M. Then there exists an integer k ≥ 1 so that, for n ≥ k,
References
- Atiyah, Michael Francis; Macdonald, I.G. (1969), Introduction to Commutative Algebra, Westview Press, ISBN 978-0-201-40751-8